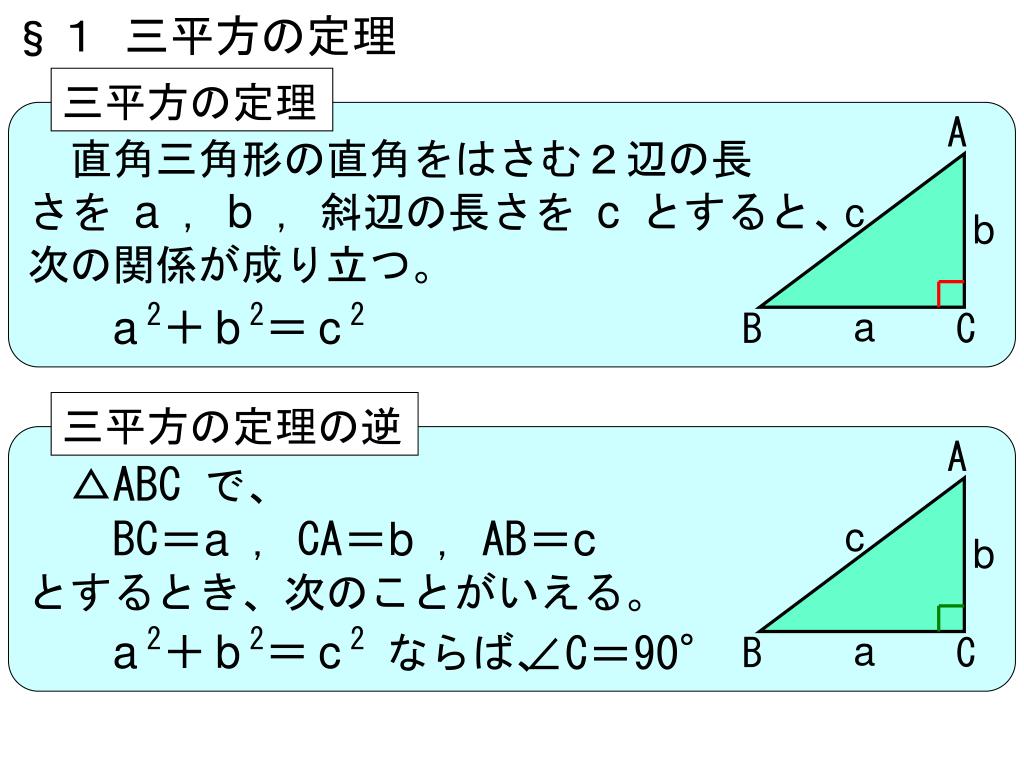
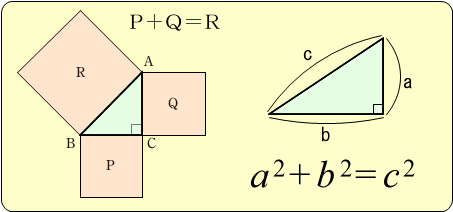
1 三平方の定理 ここでは,直角三角形の辺の長さの関係について学習してみましょう。 三平方の定理(ピタゴラスの定理) 直角三角形の直角をはさむ2 辺の長さをa,bとし,斜辺の 長さをcとすると a2+b2=c2 が成り立つ。これを三平方の定理(ピタゴラスのちなみにレ・ファ・ラを同時に叩くと暗い和音(短三和音)が響きますが、こちらは長三和音の時の直角三角形を裏返した直角三角形になります。 ↓ 図示するとこのような関係にある。 リンク Tweet Listです。ここで, 三角形 B H A が直角三角形であることを利用し, ピタゴラスの定理を書いてみます。 c 2 = a 2 sin 2 θ (b − a cos θ) 2 = a 2 b 2 – 2 a b cos

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
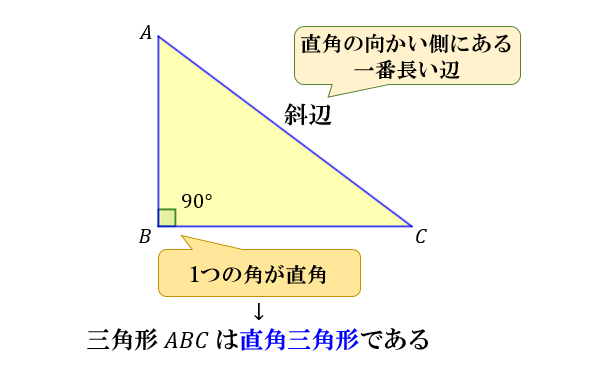
ピタゴラスの定理 直角三角形
ピタゴラスの定理 直角三角形-ピタゴラスの定理 (ピタゴラスのていり)は、 直角三角形 の3 辺 の長さの関係を表す 等式 である。 三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 三平方の定理を使って直角三角形の辺の長さを計算したい! どうも、Drリードだぞい。 中3数学では、 三平方の定理(ピタゴラスの定理)を勉強してきたよな? 簡単に復習すると、 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、



1
定理1(ピタゴラスの定理、三平方の定理) 直角三角形の斜辺の長さをa、そのほかの辺の長さをそれぞれb,cとすると、b²+c²=a²が成り立つ。 証明(これ以外にも様々な証明方法が存在する) 下の図のように一辺b+cの正方形から一辺aの正方形を取り除いた部分の面積をSとすると ピタゴラスの定理 大矢真一著 参考 直角三角形ABCを作り、それぞれの辺上に正方形を図1のように作る。 a²の中心Oを通って、ABに平行な直線KL、それに垂直な直線MNでa²を四つに切る。 また、BE,DE,AD,AB上にそれぞれ、BP=ON,PE=MO,EQ=KO,DQ=OL,DR=MO,AR=NO,AS=OL,BS=KOとなるようなP,Q,R,Sをとり、これらの △ABC と 合同 な4個の三角形を図のように並べると、外側に一辺が a b の 正方形 (以下「大正方形」)が、内側に一辺が c の正方形(以下「小正方形」)ができる。 (大正方形の面積)=(小正方形の面積)(直角三角形の面積)× 4
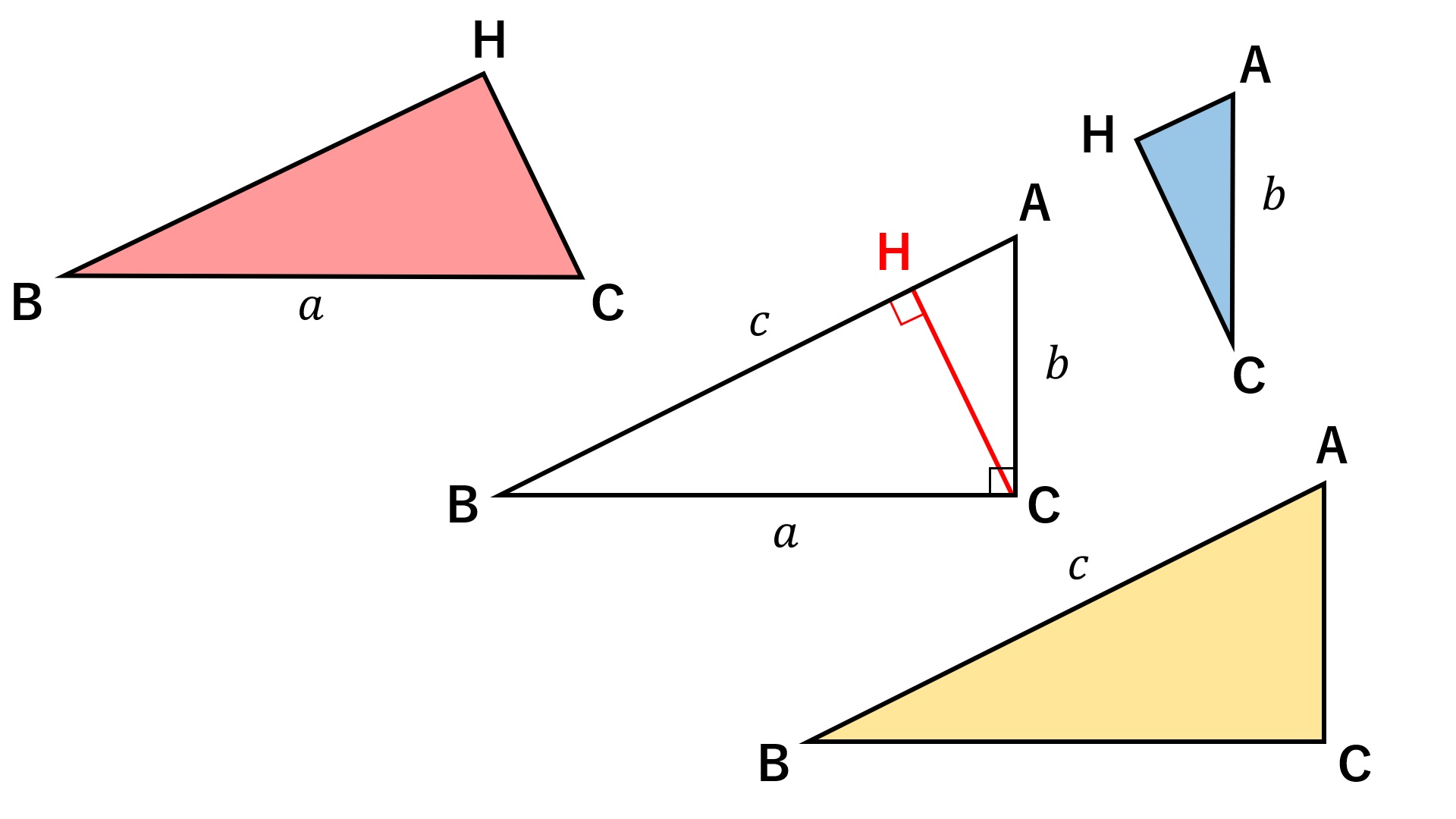
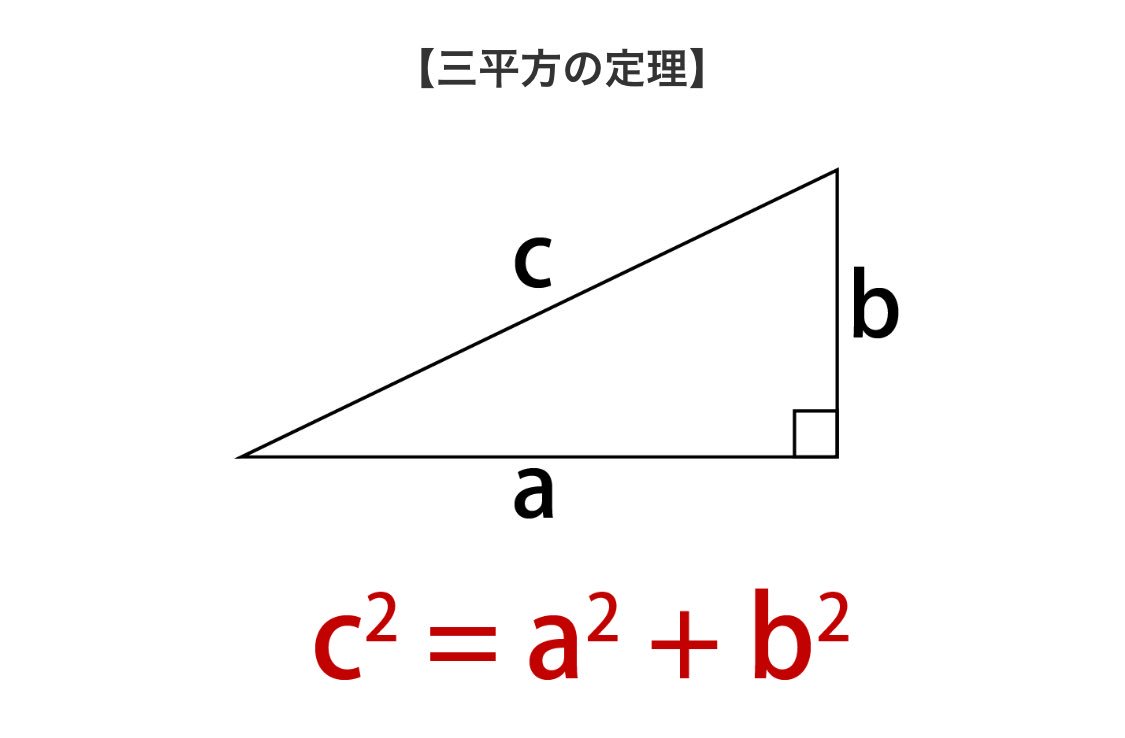
三角関数(Trigonometric Function) 1 ピタゴラスの定理 直角三角形(right triangle) は,測量の基本と言える.直角三角形でない三角形も存在するが,どん な三角形でも補助線を設けることで,二つの直角三角形に分割することが出来る.ここが重要なポイ2つの直角三角形ACH とBCH において,ピタゴラスの定理(B)を適用すると, sin sin sinxA ,sin sin sinxB であるので, sin sin sin sinA B となる。 同様に, sin sin sin sinB C であるから定理が成り立つ直角三角形の直角を挟んだ2辺の長さをaとb、直角に対する斜辺 (もっとも長い辺)の長さをcとすると (図Math001)、つぎの等式が成立ちます。 これを「三平方の定理」あるいは「ピタゴラスの定理」と呼びます。 三平方の定理 a 2 b 2 = c 2 図Math001
ピタゴラスの定理を使って、良い比率の三角形を無限に生み出す 数学 Tweet Pocket ピタゴラスの定理(または三平方の定理)は、誰もが小学生や中学生の頃から知っている馴染み深い定理だろう。 ピタゴラスの定理を使って「3対4対5」など三辺の直角三角形でもいえるのか、普通の三角形ではちょっと無理そうだとか 考えを広げていけるのが、凡人との違い? では、色々な直角三角形ではどうなるかを確認してみよう。 三平方の定理が成り立つことを確認する §3.ピタゴラスの定理の確認 ピタゴラス数:直角三角形の基本(3:4:5) 有名な「ピタゴラスの定理」(三平方の定理)は、「直角三角形 に おいて、最も長い辺の二乗は、最も短い辺と、次に短い辺の二乗の和と等しい」。 というものですね? なお、ピタゴラス(紀元前5年~紀元前496年)は古代ギリシャの数



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
2 特殊な形の三角形で利用される三平方の定理 21 直角二等辺三角形:角度が45°の直角三角形;そこで,ピタゴラスの三角形を利用してみよう. 底面の二等辺直角三角形を少しだけ変形し, A=436度,B=464度の直角三角形でよいことにすれば, 辺長を a:b:c=:21:29 と整数比率にできる. これでは,二等辺三角形ではなくなってしまう. しかし,底面と側面とを正確に同じ寸法三平方の定理とは、直角三角形の3辺の長さの関係を表す公式の事を言います。 また、別名「ピタゴラスの定理」とも呼ばれています。 この呼び方の方が有名でしょうか。 古代中国でもこの定理は使われていて、それが日本に伝わり、江戸時代には鉤股弦




三平方の定理 おやじさん ネット



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ
三平方の定理 ピタゴラスの三角形 直角三角形では、斜辺が5cmなら、隣辺は自動的に 3cmと4cmになるのでしょうか? 数学 数学 直角三角形以外の三角形の問題には正弦定理や余弦定理を使いますが、そこで出てくるsinAやcosBやtanC はどこを何を指してるんですか? 数学 3平方 の定理で、直角二もくじ 1 三平方の定理の内容:直角三角形と辺の長さの関係 11 分からない辺の長さを計算できる三平方の定理; 3:4:5の三角形で,本当に直角ができるのでしょうか。 三角形の辺の長さの比と角の大きさには,どんな関係があるのでしょうか。 3:4:5は,斜辺の対角が直角です。このことは,三平方の定理として知られています。 3:4:5



1




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
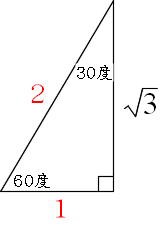
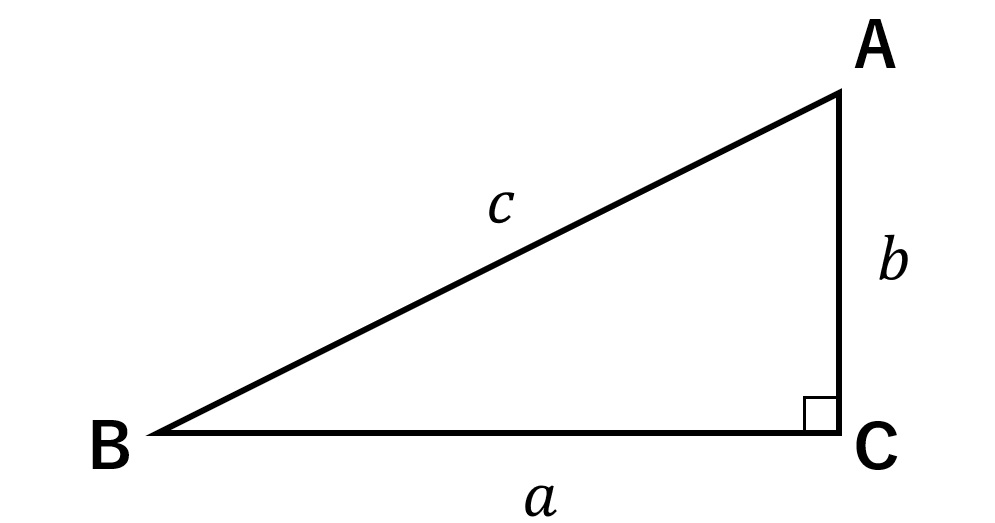
三平方の定理(ピタゴラスの定理) ∠ACB=90°となる直角三角形ABCにおいて,各辺の長さを, BC = a , CA = b , AB = c とすると, a 2 b 2 = c 2 の関係が成り立つ.この関係を 三平方の定理 あるいは ピタゴラスの定理 という. 証明 直角三角形の3辺a,b,cはa 2 b 2 =c 2 が成り立つ。 中学校で習う周知のピタゴラス定理だ。3辺が345の比は直角三角形になることを知っていた古代のエジプト人は、12等分した紐から直角を作り出していた。特別な直角三角形は 三角定規の $\textcolor{blue}{2}$ 種類 になります。 ① $\textcolor{blue}{30°,60°,90°}$ POINT:正三角形の半分 正三角形の $1$ 辺の長さを②とすると、$1$ 辺はその半分なので①となります。残り $1$ 辺を三平方の定理を使って求めると、




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



直角三角形の辺の長さ 合同条件 面積について アタリマエ
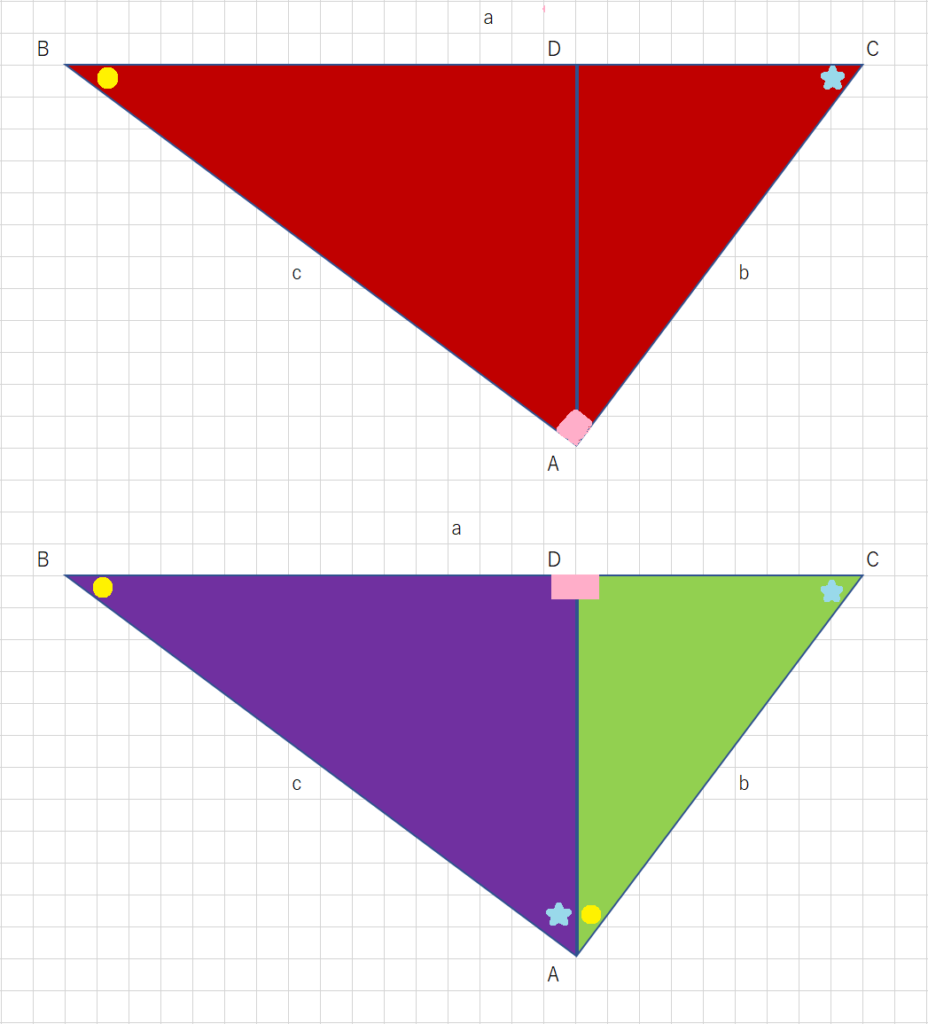
直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係は ピタゴラスの定理 (三平方の定理)と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス (cBC570cBC500)が発見したかどうか確証があるわけではありません。 この三平方の定理(ピタゴラスの定理)とは何かっていうと、 直角三角形の3つの辺の関係を表した公式 なんだ。 もうちょっと具体的にいうと、直角三角形には、 斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい っていう関係があるんだ。楔(くさび)のような形をした四角形 ${\rm DAEB}$ の面積を考えてみよう.これは二つの直角二等辺三角形からできていて,面積は $\dfrac{a^2}{2}\dfrac{b^2}{2}$ である.ところでこの図をよくよく見つめると,実は ${\rm AB}$ と ${\rm DE}$ は垂直であることが分かる.そのことから,四角形 ${\rm DAEB}$ の




三平方の定理の証明と使い方



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド
まずは、ピタゴラスの定理(三平方の定理)をおさらい ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c²直角三角形で斜辺を直径とする半円が内接していて他の2辺を直径とする半円は外接している。 タレスの定理より直角三角形の各頂点は斜辺の半円の円周上にある。 円の面積は半径の自乗に比例するので、ピタゴラスの定理より、斜辺の半円と、他の2辺の半円の和の面積は等しい。 斜辺の みなさんもピタゴラスの定理をご存知ですよね? 直角三角形の三平方の定理です。中学校のときに、その証明方法を習ったはずですよね。でも、その証明方法は100通り以上あるのだそうです。わたしも驚きました。 わたしが自分でできるうちの5通りを下の方に書いておきます。 (実は




ピタゴラスの第2定理発見 三平方根の定理 直角三角形の菅数論の定理 発想力教育研究所 素数誕生のメカニズム
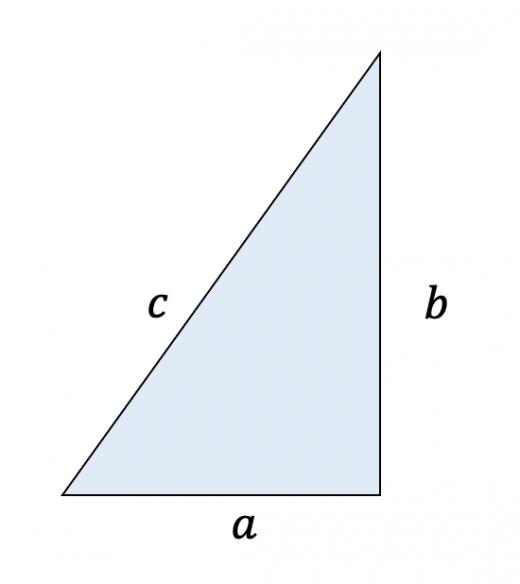



直角三角形の定義とさまざまな公式 高校数学の美しい物語
三平方の定理の証明|直感的に分かる図で解説します 管理人 5月 23, / 5月 27, 三平方の定理は直角三角形の辺の長さに関する定理ですが、今後、図形だけではなく関数などあらゆる分野でも利用することになる重要な定理です。 今回は三平方の定理直角三角形 親トピック 三角形 三角形 平面図形 三角法 幾何 数学 直角三角形 ピタゴラスの定理(三平方の定理)の証明 ブック Bunryu Kamimura 円周角の定理 ブック Bunryu Kamimura 直方体の対角線 ワークシート Tottio 底面が正方形の四角錐 ワークシート Tottio 改訂版 三角柱を切断した立 ピタゴラスの定理=三平方の定理 は、 直角三角形の90°の角を挟む辺をそれぞれ2乗し、足す=90°の角の対辺の2乗 だったと思います。 ナイス!




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
よって直角三角形において直角の対辺の上の正 方形は直角をはさむ2辺の上の正方形の和に等し い。これが証明すべきことであった。 3ピタゴラスの定理の証明法の分類 多数のピタゴラスの定理の証明法が存在するが,証明の 方法で大きく分類すると,ピタゴラスの定理 図のような3つの辺の長さが,それぞれa, b, c である 三角形ABCにおいて, B A C a b c 角Cが90 の直角三角形⇐⇒ a2 b2 = c2 体験授業(数学) 7/ 78直角三角形なら正方形を半分にしても成立することがわかっています。 では、半分よりももっと小さくした場合、他の長方形の比率はどうなってくるのでしょうか。 この図のようにEをとると、同じ比率の長方形が自然にできてピタゴラスの定理が成立します。 「水色の平行四辺形=二つのクリーム色の平行四辺形の和」 「はずす」 この図を見ると、平行線の




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




三平方の定理 自動計算サイト
ピタゴラスの定理とは、直角三角形の底辺の2乗と高さの2乗の合計が、斜辺の2乗に等しいという定理です。 この定理は、建築設計で頻繁に使います。 また構造力学や構造設計でも、ピタゴラスの定理を使い、材の長さや内力の計算をします。 今回はピタゴラスの定理の意味、定理の証明、3:4:5の関係、三平方の定理との違いについて説明します。 建築で使う補足:ピタゴラス数(整数の話題) 一般に,三つの自然数の組 ( a, b, c) (a,b,c) (a,b,c) が三平方の定理の式 a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 を満たすとき, ( a, b, c) (a,b,c) (a,b,c) を ピタゴラス数 と呼びます。 有名なピタゴラス数として,



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



Q Tbn And9gcsnbiv 7svsm 6o0qjqco66pmarde4rrmbqkrgwufvawvziomrf Usqp Cau




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




直角三角形 Twitter Search



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori



1




三平方の定理 無料で使える中学学習プリント




数学 中3 61 三平方の定理 基本編 Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理を英語で読んでみる




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく
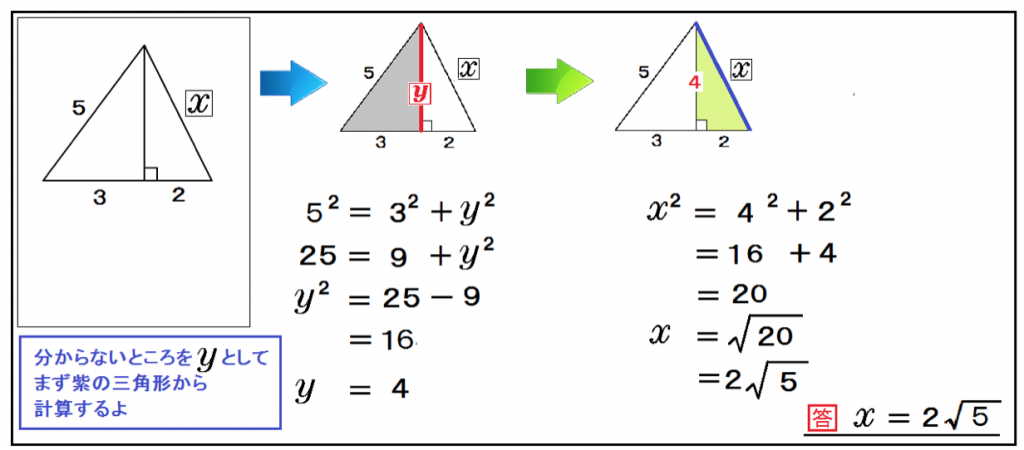



1 1 ルート2 三角形



ピタゴラスの定理の簡単な証明方法ありますか Quora
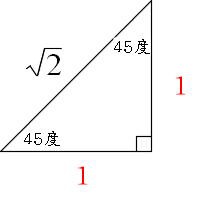



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
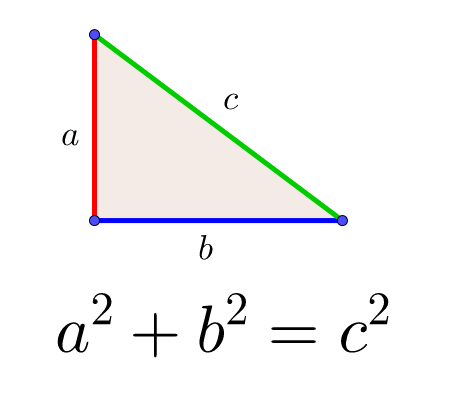



三平方の定理の証明2 4つ直角三角形と真ん中の四角 キソカラ



見えますか タイルの模様からピタゴラスの定理 Note Board



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook



中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




直角三角形 Wikipedia




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
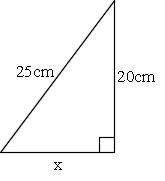



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ



ピタゴラスの定理が証明できた



直角三角形 Twitter Search




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース




三平方の定理 ピタゴラスの定理




三平方の定理を直角三角形二つで証明 Youtube




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




コラム ピタゴラスの定理 江戸の数学




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



1




Textbook T12 C01




三平方の定理の証明と使い方




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか Yahoo 知恵袋




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



6 改めてサンキュー 直角三角形 オトナのための中学数学 天狼院書店




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



Python 三平方の定理 Unpyside




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




大工の算数 ピタゴラスの定理 小屋をつくった16年暮らした
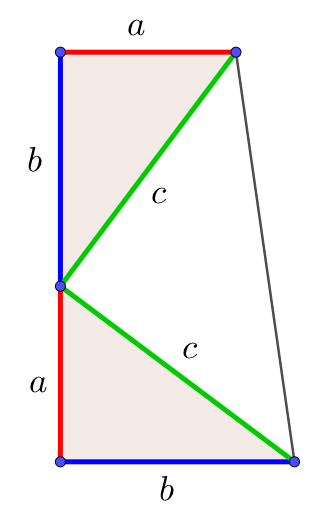



三平方の定理の証明3 大統領の台形 キソカラ
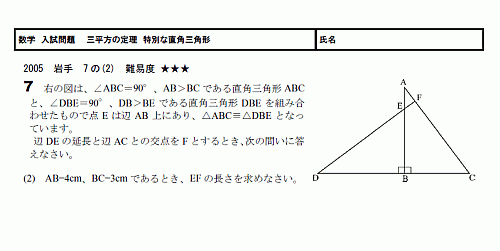



三平方の定理 スタディーx




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ
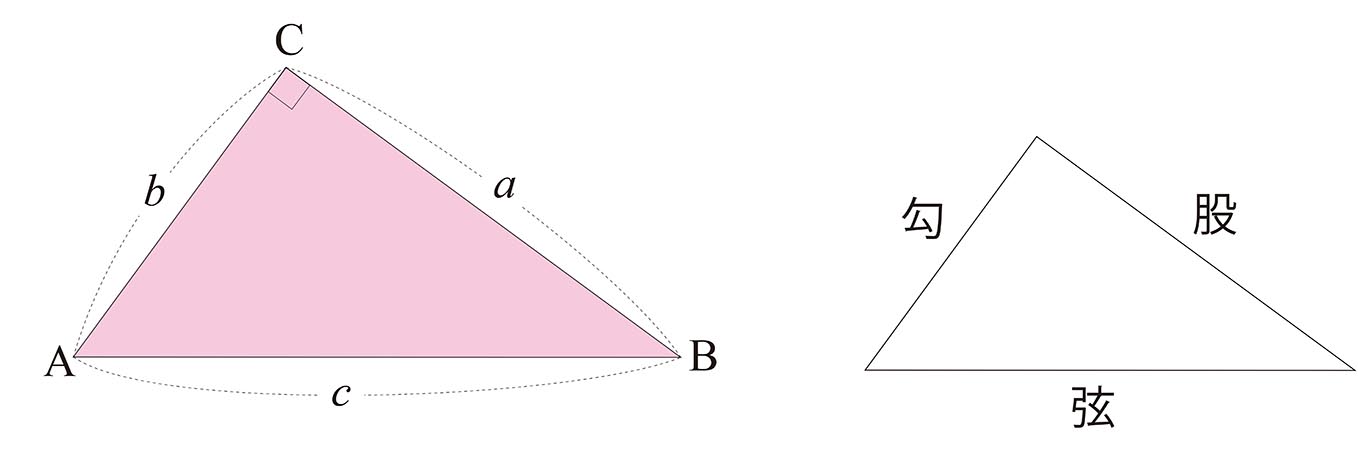



コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




三平方の定理 覚えておきたい基本公式を解説 数スタ




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
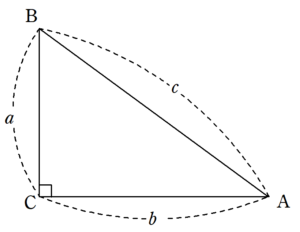



三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも
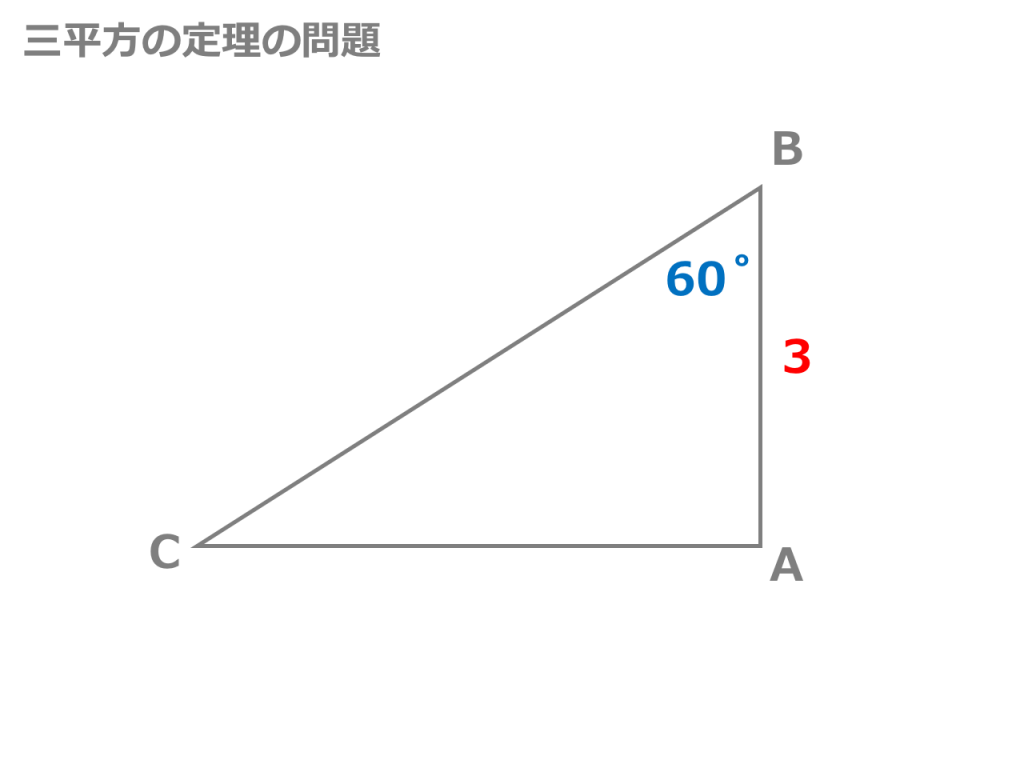



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




三平方の定理で辺を求める Youtube



三平方の定理




三平方の定理の証明と使い方



三平方の定理の導入 Geogebra



0 件のコメント:
コメントを投稿